На главную страницу

Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
Алгебра 11 класс

 на главную
на главную
Cтандартный вид числа
Поддержать сайтВ задачах по физике часто приходится работать с очень большими и очень малыми величинами.
Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?
Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.
Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число «10» в различных степенях.
- 10−2 =
=1 102
= 0,01 (более подробно об отрицательной степени можно прочитать в уроке 9 класса «Отрицательная степень»)1 100 - 10−1 =
=1 101
= 0,11 10 - 100 = 1
- 101 = 10
- 102 = 100
- 103 = 1000
- …
Вспомним, что при умножении целого числа на 10, 100, 1000 и т.д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..
- 5 · 10 = 50
- 27 · 100 = 2 700
- 18 · 1000 = 18 000
Теперь запишем тоже самое, используя определение степени.
- 5 · 10 = 5 · 101 = 50
- 27 · 100 = 27 · 102 = 2 700
- 18 · 1000 = 18 · 103 = 18 000
При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.
- 13 000 : 100 =
= 13013 000 100 - 50 : 10 =
= 550 10
Для десятичных дробей действует схожее правило умножения на 10, 100, 1000. При умножении десятичной дроби на 10, 100, 1000 и т.д. мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д...
- 5,7 · 100 = 570
- 7,013 · 10 = 70,13
- 68,3 · 1000 = 68 300
С помощью степени можно записать вычисления выше следующим образом:
- 5,7 · 100 = 5,7 · 102 = 570
- 7,013 · 10 = 7,013 · 101 = 70,13
- 68,3 · 1000 = 68,3 · 103 = 68 300
При делении на 10, 100, 1000 и т.д. перемещаем запятую влево.
- 6,7 : 10 =
= 0,676,7 10 - 0,15 : 100 =
= 0,00150,15 100
С помощью определения отрицательной степени можно записать вычисления выше следующим образом:
- 6,7 : 10 =
= 6,7 · 10−1 = 0,676,7 10 - 0,15 : 100 =
= 0,15 · 10−2 = 0,00150,15 100
Стандартный вид числа
Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.
Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:
где 1 ≤ a < 10 и n — натуральное число.
Такая запись называется — стандартный вид числа.
При этом число
«n»
называют порядком числа «a».
Из определения выше важно понять, что степень, в которой стоит «10», в стандартном виде числа называется порядком.
Теперь к примеру. Пусть нам дано число «5 600» и требуется записать его в стандартном виде.
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».
В числе «5 600» первая цифра справа — «5». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.

Значит, чтобы из «5,600» получить «5600» нам нужно умножить «5,600» на «1000». Запишем полученное преобразование.
Теперь запишем «1000» с использованием степени.
Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.
= 5,6 · 103
Таким образом «5 600» в стандартном виде будет выглядеть следующим образом:
Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно. Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.
Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь «0,017».
Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от «1» до «9».
В десятичной дроби «0,017» вначале идет «0». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от «0».
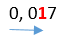
Это цифра «1». Посчитаем сколько знаков (цифр) стояло от запятой до цифры «1», включая саму цифру «1».
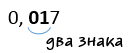
Получается два знака. Начнем записывать «0,017» в стандартном виде. Перенесем запятую и поставим ее справа от «1».
Ответим себе на вопрос: "На что нужно умножить или разделить «1,7», чтобы получить изначальное число «0,017» ?". Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится влево.
Выходит, чтобы из «1,7» сделать 0,017», нужно «1,7 разделить на «100» (чтобы перенести запятую на два знака влево).
Запишем это деление на «100», используя обыкновенную дробь.
| 1 |
| 100 |
С помощью отрицательной степени запишем окончательный вид числа «0,017» в стандартном виде.
| 1 |
| 100 |
1,7 · 10−2
Примеры решения задач
на запись числа в стандартном виде
Разбор примера
Определить порядок числа, выражающего значение физической константы:
1) масса покоя электронаme = 9,1093897 · 10−31
Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень,
в которой стоит «10».
В данном примере «10» стоит в
степени
«−31».
Значит, порядком массы покоя электрона является «−31».
Разбор примера
Записать в стандартном виде и определить порядок числа k, выражающего физического константу:
2) постоянная ФарадеяF = 96485,309 Кл/моль;
По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».
Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра «9».
Зададим себе вопрос: «На что нужно умножить «9,6485309», чтобы получить «96485,309» ?» Посчитаем количество знаков (цифр), на которое требуется перенести запятую в «96485,309», чтобы получить «96485309».
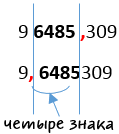
Получается «4» знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:
Порядком числа «9,6485309 · 104» является степень, в которой стоит «10». Следовательно, порядок «k = 4».
3) Постоянная Лошмидта
n0 = 2686763 · 10 26
Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:
2,686763 · 10 26 · 10…
Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую, чтобы из «2,686763» получить «2686763».
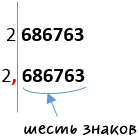
Значит, чтобы получить из «2,686763» нужно изначальное число «2686763» умножить на «106».
2,686763 · 10 26 · 106
Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».
Другие примеры записи чисел в стандартном виде
- 0,52 = 5,2 · 10 −1
- 401 = 4,01 · 10 2
- 60,756 = 6,0756 · 101
- 0,00123 = 1,23 · 10−3
Ваши комментарии
Оставить комментарий:
0,0245=
0,000000985
0,002=
0,00003598=
2500000000=
36800000000000000=
536700000=
520000=
 Ответить
Ответить
Ответ для Ирина Колесник
0,0000000058=5,8 · 10-9
0,0245=2,45 · 10-2
0,000000985= 9,85 · 10-7
0,002=2 · 10-3
0,00003598=3,598 · 10-5
2500000000=2,5 · 109
36800000000000000=3,68 · 1016
536700000=5,367 · 108
520000= 5,2 · 105
 Ответить
Ответить
Ответ для Кирилл Гуменюк
Ответ: порядок числа 0,01а равен -5.
 Ответить
Ответить